[Leet Code] 876. Middle of the Linked List
2025. 9. 1. 23:55ㆍCS & Algorithm/문제풀이
문제
https://leetcode.com/problems/middle-of-the-linked-list
메서드 실행 코드
// 단일 연결 리스트 노드 정의
class ListNode {
int val;
ListNode next;
ListNode() {}
ListNode(int val) { this.val = val; }
ListNode(int val, ListNode next) { this.val = val; this.next = next; }
}
// 실행 테스트
public class Main {
public static void main(String[] args) {
// 연결 리스트 [1,2,3,4,5] 만들기
ListNode head1 = new ListNode(1);
head1.next = new ListNode(2);
head1.next.next = new ListNode(3);
head1.next.next.next = new ListNode(4);
head1.next.next.next.next = new ListNode(5);
// middleNode 호출
Solution sol = new Solution();
ListNode middle1 = sol.middleNode(head1);
// 연결 리스트 [1,2,3,4,5,6] 만들기
ListNode head2 = new ListNode(1);
head2.next = new ListNode(2);
head2.next.next = new ListNode(3);
head2.next.next.next = new ListNode(4);
head2.next.next.next.next = new ListNode(5);
head2.next.next.next.next.next = new ListNode(6);
ListNode middle2 = sol.middleNode(head2);
}
}
문제 내용 요약
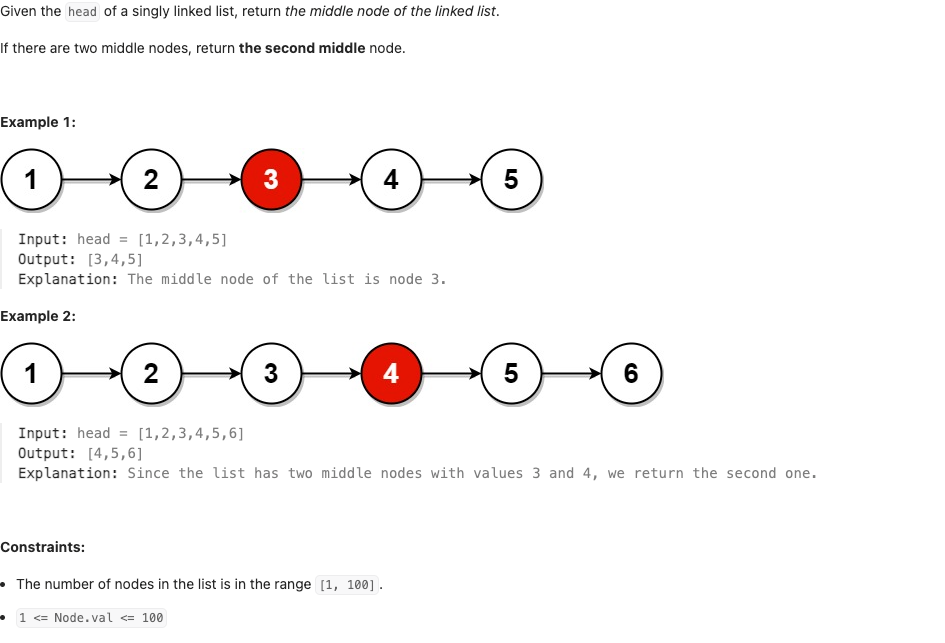
- 연결 리스트의 head가 주어진다.
- 목표: 연결 리스트의 중간 노드를 반환한다.
- 짝수 개의 노드가 있다면, 두 개의 중간 노드 중 두 번째를 반환한다.
내가 작성한 답변
길이로 구하는 방식
class Solution {
public ListNode middleNode(ListNode head) {
// 1. 길이 구하기
int length = 0;
ListNode temp = head;
while (temp != null) {
length++;
temp = temp.next;
}
// 2. 중간 인덱스 구하기
int mid = length / 2 + 1; // 홀수/짝수 모두 처리 가능
// 3. mid번째 노드로 이동
temp = head;
for (int i = 1; i < mid; i++) {
temp = temp.next;
}
return temp;
}
}
풀이 강의 답변
포인터 사용
class Solution {
public ListNode middleNode(ListNode head) {
ListNode middle = head;
ListNode end = head;
while (end != null && end.next != null) {
middle = middle.next;
end = end.next.next;
}
return middle;
}
}
정리
- 두 방법 모두 시간 복잡도는 O(n)
- 길이 구하는 방식: 코드가 직관적이고 초심자 친화적
- 두 포인터 방식: 메모리 효율적이고 리스트를 한 번만 순회하므로 더 최적화됨
- 코딩테스트에서는 두 포인터 풀이를 쓰는 경우가 많음
'CS & Algorithm > 문제풀이' 카테고리의 다른 글
| 120923. 연속된 수의 합 (0) | 2025.09.10 |
|---|---|
| [백준] 2745. 진법 변환 (0) | 2025.09.02 |
| [Leet Code] 1342. Number of Steps to Reduce a Number to Zero (0) | 2025.09.01 |
| Lv.0 주사위 게임2 (1) | 2023.12.07 |
| Lv.0 코드 처리하기 (1) | 2023.12.06 |